Espacio Geográfico. Dr. Luis Ignacio Hernández Iriberri

Empecemos por el Canevá de la Proyección Equirrectangular.  Artículo, 2012.

Dr. Luis Ignacio Hernández Iriberri.

“Espacio Geográfico”, Revista Electrónica

de Geografía Teórica.

http://espacio-geografico.over-blog.es/

30 ene 12

Ahí está la Tierra, la superficie de esa esfera, un plano curvo bidimensional, define el espacio terrestre en esa condición de dos dimensiones.

Conocemos la historia de Eratóstenes por la que éste determinó  el valor de su perímetro en 40,000 km; pero aún más, dicha esfera tiene una simetría dada en función de un eje de rotación que le da a ese espacio una bipolaridad, que la divide en dos hemisferios por el ecuador.

El problema que se le planteó a Hiparco, fue la transformación de esa esfera en un plano, con arreglo a las proporciones de sus medidas reales.

E Hiparco decidió el desarrollo de la esfera en un plano, de acuerdo con el movimiento de rotación, de modo que la longitud del plano a escala, tendría el equivalente a 40,000 km, teniendo al ecuador  como línea media.  Por definición, quedando a la vista de manera directa la distancia entre los dos polos, el ancho del plano sería entonces, equivalente a 20,000 km.

Y así quedó definida la Proyección Equirrectangular de Hiparco (aun cuando estrictamente, tal desarrollo no es propiamente una proyección en su sentido geométrico).  La denominación de “equirrectangular” viene de la división sucesiva y proporcional en rectángulos iguales.

Luego, la esfera define una geometría de valores sexagesimales, que de inmediato en sus valores asignados en sus dos ejes de simetría esenciales, primero en el ecuador para los valores de 90º da latitud (entre 0º y 90º)

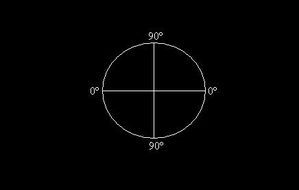
Y luego, definido ese meridiano convencional de origen en 0º, la extensión total del perímetro del ecuador dividido a ambos lados por dicho meridiano, arroja los valores de 0º a 180º al Este, e igualmente equivalente, al Oeste.

Y finalmente, se asignan los valores de coordenadas en su subdivisión exacta entre los extremos.

Por último, teniendo tal canevá como referencia, con respecto a él se trazan los continentes y rasgos de la superficie terrestre que interesen.

Este canevá, geométricamente, tiene un problema: todo va bien, hasta que se trazan los paralelos, los cuales corresponden a círculos menores al ecuador, y, por lo tanto, cuyo perímetro ha de ser cada vez menor según su proximidad a los polos, lugar último en que se convierten en un punto; y resulta que éstos, e incluso los puntos mismos de los polos, se extienden en una longitud igual a la del ecuador, introduciendo una deformación en el sentido de las longitudes, cada vez mayor conforme el valor latitudinal hacia los polos.

No obstante, esa deformación propia a esta Proyección Cartográfica, ello no quiere decir que ésta “no sirva”, sino sólo quiere decir que esa proyección es así, y con toda sencillez, es absolutamente válida y correcta, teniendo sólo presente el pronunciado anamorfismo que se produce; siendo exactamente lo mismo para todas las proyecciones cartográficas, cada una con su tipo de deformación inevitable.