Espacio Geográfico. Dr. Luis Ignacio Hernández Iriberri

Geografía Básica.  Libro Básico de Consulta, 1994 (16/).

Dr. Luis Ignacio Hernández Iriberri.

“Espacio Geográfico”, Revista Electrónica

de Geografía Teórica.

http://espacio-geografíco.over-blog.es/;

31 mar 11.

2  Cartografía.

Entre los griegos, conocedores ya de las propiedades espaciales de la esfericidad de la Tierra y de su simetríaa bipolar, se avanzó ahora sobre el problema de su magnitud.

Tocó a Eratóstenes en el siglo III ane, encontrar el método para determinar el perímetro de la esfera terestre.  En realidad, no podía partir más que del punto en que Diceraco le heredó los estudios del espacio terrestre: el conocimiento del punto de la Tierra de sombra cero in situ del gnomon y su valor angular de latitud correspondiente.

Eratóstenes reflexionó en que, siendo la Tierra una Esfera, un ángulo medido en el gnomon en algún punto de la Tierra, sería proporcional a una distancia de segmento de círculo sobre el mismo meridiano, entre ese punto, y el punto de sombra cero del gnomon en la fecha del solsticio; tanto como el ángulo total del círculo, lo sería a su perímetro.  Es decir, que habría una relación directamente proporcional entre el ángulo del gnomon, y una distancia; u los 360º del círculo, y su perímetro. (fig. 69).

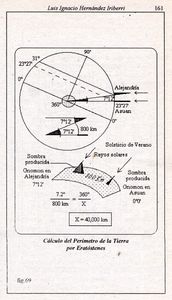
Se considera que el ángulo medido por Eratóstenes en el gnomon, fue de 7.2º, y que la distancia del arco de medido entre el lugar de la posición del gnomon y el Trópico ( sombra cero del solsticio), sobre el mismo meridiano, sería, en unidades actuales, de unos 800 km, de manera que si 7.2º correspondían a 800 km, 360º habrían de corresponder al perímetro de la Tierra, que, resolviendo la operación con los datos obtenidos, da un valor de 40,000 km.

Físicamente, hemos visto, la noción del espacio era de una naturaleza bidimensional; filosóficamente, de acuerdo con la autoridad de Aristóteles para ese entonces, el espacio terrestre era la superficie, en este caso, de la esfera terrestre.  Conocido el valor del perímetro de dicha esfera, la medida del espacio terrestre (el valor de su extensión superficial), era algo plenamente determinado.

Representar los rasgos de la Tierra en un Globo Terráqueo como lo hizo Crates en el siglo II ane, resultaba algo sin dificultad.  La incomodidad, era transportar el Globo Terráqueo mismo.  De ahí que se planteó el problema de representar los rasgos del Globo Terráqueo, en un plano o mapa, a su escala.

La transformación geométrica de la esfera en un plano no tiene una solución única: o el plano sufre cortaduras conservando los rasgos verdaeros de los continentes, o se conserva la continuidad en el plano, sacrificando la figura verdadera de los continentes con ciertas deformaciones.  Así empezó la búsqueda de un sistema de proyección cartográfica que fuese idóneo.

Hiparco (s.II ane), asumió por primera vez la tarea, construyendo una primera representación, mediante una Proyección Cartográfica No-Verdadera (fig. 70).  Es decir, simplemente trazó un semimeridiano central (la mitad del perímetro de la Tierra), a escala, dividiéndolo en partes iguales, por cuya parte central trazó enteramente el ecuador, a su vez, a escala (resultando del doble de longitud, por lo tanto, que el semimeridiano central), y trazó cada uno de los paralelos, como líneas de igual magnitud que el ecuador, y paralelas a este.

El ecuador lo dividió a su vez, proporcionalmente en las mismas partes que el semimeridiano central, quedando la red de paralelos y meridianos como una cuadrícula de rectángulos iguales; de donde dicha Proyección tomo su nombre como: Proyección Equirectangular.

Al configurar los continentes, puede apreciarse la enorme deformación que se produce en sentido longitudinal, siendo tanto mayor dicha deformación, cuanto más nos aproximamos hacia los polos, debido a que los círculos paralelos rectificados, cuanto más próximos a los polos, deberían tener cada vez una mayor extensión o longitud métrica.  Dichas deformaciones no significan que la Proyección o el mapa “estén mal”, sino simplemente que así es esa Proyección.

Poco después, el mismo Hiparco diseñó un modelo de proyecciones verdaderas, o proyecciones geométricas planas.  Imaginó proyectar la red de paralelos y meridianos, conocido también como canevá, sobre un plano tangente a la Tierra en tres posibles posiciones: 1) tangente al ecuador, 2) tangente a los polos, y 3) tangente en cualquier punto intermedio entre el ecuador y los polos, o posición oblicua o meridiana.

A la vez, cada una de esas tres posibles proyecciones de acuerdo al la posición del plano, se dividió en tres tipos de acuerdo con la posición, ahora, del foco de proyección: 1) en el centro, o gnomónico (fig. 71); 2) diametralmente opuesto al punto de tangencia, o estereográfico (fig. 72); y 3) en el infinito, opuesto al plano de proyección, u ortográfico.  De modo que se tendrá la siguiente serie de Proyecciones Cartográficas posibles:

1       Gnomónica Ecuatorial

2       Gnomónica Polar

3       Gnomónica Oblicua.
 

4       Estereográfica Ecuatorial

5       Estereográfica Polar

6       Estereográfica Oblicua.

7       Ortográfica Ecuatorial

8       Ortográfica Polar

9       Ortográfica Oblicua.

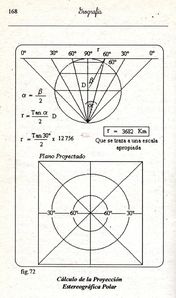
Con ello, en lo fundamental, la elaboración de los mapas estaba científicamente definida.  Si la primera Proyección, la Equirectangular, deformaba en las regiones polares en sentido longitudinal, ahora las Proyecciones Geométricas Planas eran justas sólo en las proximidades del punto de tangencia del plano de proyección.